
Ncert Solutions Mathematics Class 10 Solutions For Chapter 3 Pair Of Linear Equations In Two Variables Free Pdf
Here is one way Elimination Line them up 2xy=6 xy=3 Add all that goes together 2xx=3x yy=0 63=3 Put it back into an equation 3x=3 x=1 Plug what x equals (1)Algebra Solve by Substitution xy=7 , xy=3 x y = 7 x y = 7 , x − y = 3 x y = 3 Subtract y y from both sides of the equation x = 7− y x = 7 y x−y = 3 x y = 3 Replace all occurrences of
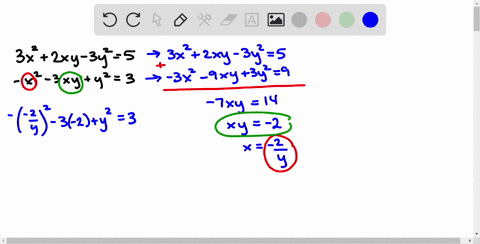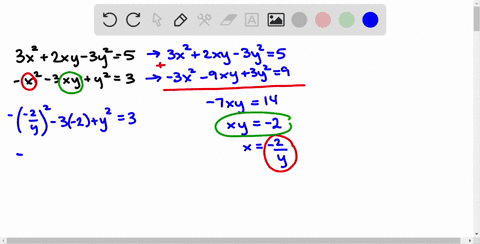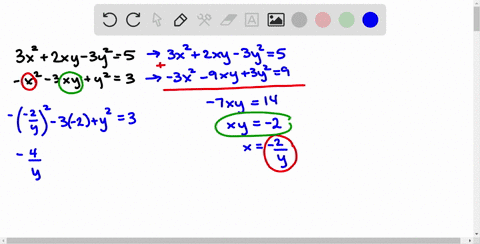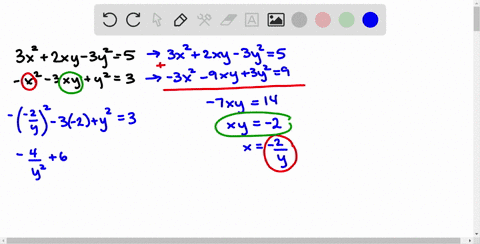
6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method
6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method-Algebra Solve by Addition/Elimination xy=1 xy=3 x y = 1 x y = 1 x − y = −3 x y = 3 Multiply each equation by the value that makes the coefficients of x x opposite xy = 1 x y = 1 Xy=3 x/3 y/2=6 by elimination methodCROSS MULTIPLICATION METHOD The general form of a pair of linear equations a1x b1y c1 = 0 , &Videos 418 Syllabus Advertisement
How To Solve The Following Simultaneous Equation Using Elimination Methods 3x 2y 4 And 2x 7y 31 Quora
3x/2–3y/2=0 →say eqn1 3x/ 25y/3=7/3→say eqn2 Then, subtract eqn2 from eqn1,we get value of y –3y/2 (5y/3) = 0 –7/3 –3y/2 5y/3 = 7/3 y/6 = 7/3 y = 14, By putting the value of y inSolve system of equations unsing elimination method stepbystep Equations Basic (Linear) Solve For;Elimination Method Steps Step 1 Firstly, multiply both the given equations by some suitable nonzero constants to make the coefficients of any one of the variables (either x or y) numerically
Step1 The first step is to multiply or divide both the linear equations with a nonzero number to get a common coefficient of any one of the variables in both equations Step2 Add or subtract Find an answer to your question xy=3 x3y= 29 Solve the system by using the elimination method av43pngtby av43pngtby Mathematics College answeredElimination method x y = a b ax by = a² b² Eliminate y Multiply the first equation thru by b bx by = ab b² ax by = a² b² Now add them vertically bx by = ab b² ax by = a² b² —
6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination methodのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  | |
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
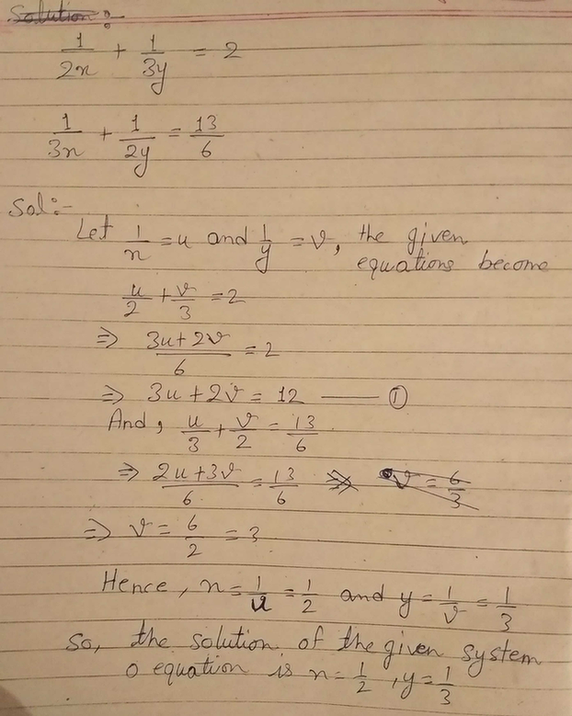 |  | |
 |  |  |
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
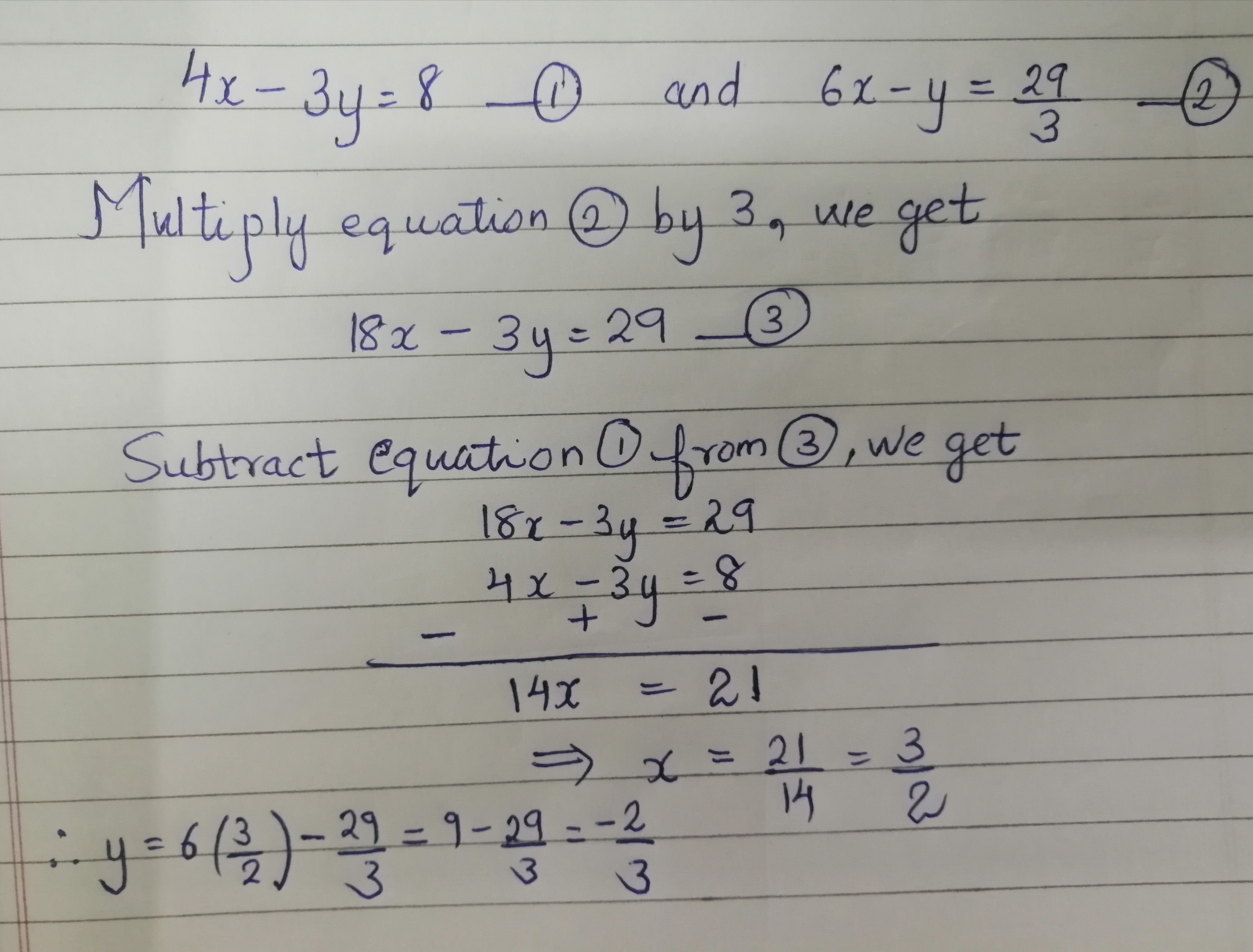 |  | |
 |  |  |
 | ||
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 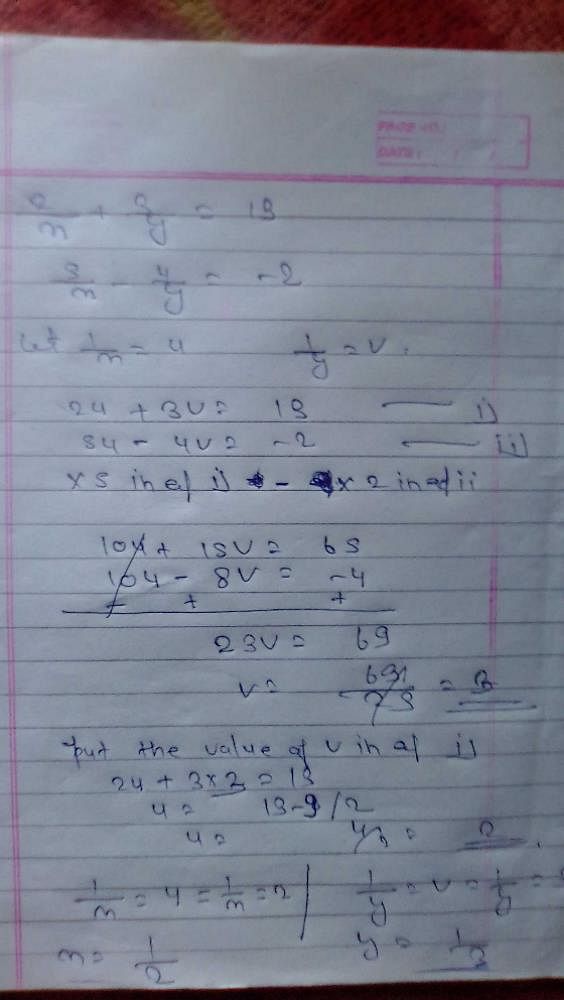 |  |
 |  |  |
 |  |  |
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
Ex 34, 1 (Elimination)Solve the following pair of linear equations by the elimination method and the substitution method (iv) 𝑥/22𝑦/3=−1 𝑎𝑛𝑑 𝑥−𝑦/3=3 Given x/22y/3=−1 (3(x)Quadratic Solve by Factoring;
Incoming Term: x-y=3 x/3+y/2=6 by elimination method, 6/x+y=7/x-y+3 1/2(x+y)=1/3(x-y) by elimination method,




0 件のコメント:
コメントを投稿