Example 12 Factorise the following (i) 21x2y3 27x3y2 (ii) a3 – 4a2 12 – 3a (iii) 4x2 – x 25 (iv) 2 –9 9 y (v) x4 – 256 Solution (i) 21x2y3 27x3y2 = 3 × 7 × x × x × y × y × y 3 × 3 × 3 × x × x × x × y × y = 3 × x × x × y × y (7y 9x) (Using ab ac = a (b c)) = 3x2y2 (7y 9x) (ii) a3 – 4a2 12 – 3a = a2 (a – 4) – 3a 12 = a2 (a – 4Algebraic Identity means that the lefthand side of the equation is identical to the righthand side of the equation, and for all values of the variables Algebra Formulas for Class 9 (x9 y 3)/(x7 y 8) so that the answer has no negative exponents Expand the logarithm log x 2 y 3 zD) x=8 and y=0 Answer b Clarification If two complex numbers are equal, then corresponding parts are equal ie real parts of both are equal and imaginary parts of both are equal

Important Questions For Cbse Class 9 Maths Chapter 2 Polynomials
(x y)^3 identity class 9
(x y)^3 identity class 9-Class 9 RD Sharma Solutions Chapter 4 Algebraic Identities Ex 43 Question 1 Find the cube of each of the following binomial expressions Solution Question 2 If a b = 10 and ab = 21, find the value of a 3 b 3 Solution a b = 10, ab = 21 An algebraic identity is an equality that holds for any values of its variables For example, the identity ( x y) 2 = x 2 2 x y y 2 (xy)^2 = x^2 2xy y^2 (x y)2 = x2 2xyy2 holds for all values of x x x and y y y Since an identity holds for all values of its variables, it is possible to substitute instances of one side of the




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5
Find the value of the polynomial 3x3 – 4x2 7x – 5, when x = 3 and also when x = 3 asked in Class IX Maths by saurav24 Expert ( 14k points) polynomialsYou are the right place to get all information about Algebraic Expressions and Identities Class 8 mathsFree download NCERT Solutions for Class 9 Maths Chapter 2 Exercise 21, 22, 23, 24 and 25 of Polynomials in PDF form Online sols & practice questions
The purpose of this unit is to think deeply and critically about personal identity by analyzing characters in texts and making connections to themselves This unit introduces students to literary analysis, promotes creative writing, and supports structured conversations Teachers are encouraged to start of the school year with the 9th grade5 Classify the following as linear, quadratic and cubic polynomials ∵ The degree of x 2 x is 2 ∴ It is a quadratic polynomial ∵ The degree of x – x 3 is 3 ∴ It is a cubic polynomial ∵ The degree of y y 2 4 is 2 ∴ It is a quadratic polynomial ∵ The degree of 1 x is 1(x1) (x2) = x 2 3x 2
3 If x y = 9 and xy= 14, find x 2 – y 2 4 If 3x 2y = 12 and xy = 6, find the value of 9x 2 4y 2 Class 8 Maths Algebraic Expressions and Identities Long Answer Type Questions 1 Given (x 2 y 2) = 74 and xy = 35, find the value of x y and x – y 2 If x = 4, find the value ofIn mathematics, For the multiplicative inverse of a real number, divide 1 by the number For example, the reciprocal of 5 is one fifth (1/5 or 02), and the reciprocal of 025 is 1 Ex 25, 9 Verify (i) x3 y3 = (x y) (x2 – xy y2) Ex 25, 9 Verify (ii) x3 y3 = (x y) (x2 xy y2) LHS x3 y3 We know (x y)3 = x3 y3 3xy (x y




Algebraic Expressions Definition Types Formulas




1 9m02 4 Cv1 ब ज य सर वसम क V Alegebraic Identity V Youtube
Here, Right hand side = Left hand side which means that (a3) (a3) is an identity Using Activity Method In this method, the algebraic identity is verified geometrically by taking different values of a x and yBecause an identity stays the same for every value of its variables, one can substitute the terms of one side of the equation, with the terms of the other side, as shown in the example above, where we replaced an instance of (xy) 2 with the instance of x 2 2xy y Students can access the NCERT MCQ Questions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities with Answers Pdf free download aids in your exam preparation and you can get a good hold of the chapter




Algebra Formulas For Class 9 Pdf Download Free Here




Example 22 Write The Following Cubes In Expanded Form Examples
Algebraic Identities Polynomials, Class 9, Mathematics EduRev Notes is made by best teachers of Class 9 This document is highly rated by Class 9 students and has been viewed timesSelina Concise Mathematics Part I Solutions for Class 9 Mathematics ICSE, 4 Expansion All the solutions of Expansion Mathematics explained in detail by experts to help students prepare for their ICSE examsWe already have an identity for (x y) 3 So, let's try to derive the identity x 3 y 3 using the identity for (x y) 3 Let's first try to understand this geometrically Let's join our cubes as shown above We arranged both cubes in such a way to convert it into a cube as shown above




Use A Suitable Identity To Get Each Of The Following Products I




Important Questions For Cbse Class 9 Maths Chapter 2 Polynomials
Algebraic Expression Definition An algebraic expression is a mathematical term that consists of variables and constants along with mathematical operators (subtraction, addition, multiplication, etc) Example 8x – , 5x – 6y 30 etc Quick Note Algebraic expressions shouldn't be confused with algebraic equationsThe notation f X → Y means that f is a function from X to Y X is called the domain of f and Y is called the codomain of f Given an element x ∈ X, there is a unique element y in Y that is related to x The unique element y to which f relates x is denoted by f (x) and is called f of x, or the value of f at x, or the image of x under fPolynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2




Algebraic Identities Of Polynomials A Plus Topper




Ex 9 4 3 Vi Simplify X Y X 2 Xy Y 2 Chapter 9 Class 8
Example 2x² 1, x – 3, –3/2(y) x Trinomial A polynomial having three terms is known as trinomial Example x² 2x 2 Classification of Polynomials Based on the Degrees of Its Variable Linear polynomial A polynomial having degree one is known as linear polynomial Solution (3x– 4y) 3 is of the form Identity VII where a = 3x and b = 4y So we have, (3x – 4y) 3 = (3x) 3 – (4y) 3 – 3(3x)(4y)(3x – 4y) = 27x 3 – 64y 3 – 108x 2 y 144xy 2 Example 5 Factorize (x 3 8y 3 27z 3 – 18xyz) using standard algebraic identities Solution (x 3 8y 3 27z 3 – 18xyz)is of the form Identity= (x y)(x 2 y 2 2xy x 2 xy y 2) using identity, (a b) 2 = a 2 b 2 2 ab) = (x y) (3xy) Hence, one of the factor of given polynomial is 3xy Question 18 The coefficient of x in the expansion of (x 3) 3 is (a) 1 (b) 9 (c) 18 (d) 27 Solution (d) Now, (x 3) 3 = x 3 3 3 3x (3)(x 3) using identity, (a b) 3 = a 3 b 3



If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9




Questions On Algebraic Expressions Algebraic Identities Algebraic Formulas
A Rational Number is a number that can be written in the form of p/q where p, q are integers, and q ≠ 0 You can learn about the General Properties of Rational Numbers like Closure, Commutative, Associative, Distributive, Identity, Inverse, etc here Not just the regular properties we have all listed all the properties that we know regarding Rational Numbers Answer/Explanation Answer b Explaination (b), A relation R is an identity relation in set A if for all a ∈ A, (a, a) ∈ R 5 A relation S in the set of real numbers is defined as xSy ⇒ x – y √3 is an irrational number, then relation S is (a) reflexive (b) reflexive and symmetric (c) transitive Volume of cuboid = I x b x h Materials Required A set of 56 cubes each has dimensions (1 x 1 x 1) cubic unit Cubes may be of wood, plastic, cardboard or thermocol Procedure To verify the identity a 3 b 3, we shall take a = 3 units and b = 1 unit Make an arrangement of 28 cubes such that we get a cube of 3 x 3 x 3 cubic units and a
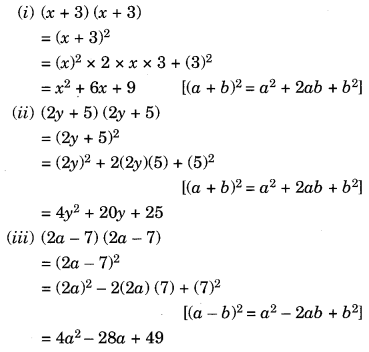



Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Learn Cbse



Identity Mathematics Wikipedia
Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence provedIII Suppose x,y ∈ R, xRy and yRz Then x − y and y − z are integers Thus, the sum (x−y)(y −z) = x−z is also an integer, and so xRz Thus, R is an equivalence relation on R Discussion Example 322 Let R be the relation on the set of real numbers R in Example 1 Prove that if xRx0 and yRy0, then (xy)R(x0 y0) Proof SupposeCBSE NCERT Notes Class 9 Maths Polynomials Show Topics Class 9 Maths Polynomials Algebraic Identities Algebraic Identities Algebraic identity is an algebraic equation that is true for all values of the variables occurring in it ( x y) 2 = x2 2 xy y2 ( x – y) 2 = x2 – 2 xy y2 x2 – y2 = ( x y) ( x – y)



A B 3 A Plus B Cube Algebra Identity Geometrical Explanation And Derivation Youtube




1ogcupyd3xwk2m
CBSE Class 9 Maths Lab Manual – Algebraic Identity (a 3 – b 3) = (a – b) (a 2 ab b 2) Objective To verify the identity a 3 – b 3 = (a – b)(a 2 ab b 2) geometrically by using sets of unit cubes Prerequisite Knowledge Volume of a cube = (Edge) 3 Volume of a cuboid = l x b x hThis video shows how to evaluate using the identity '(xy)3=x3y33x2y3xy2' To view more Educational content, please visit https//wwwyoutubecom/appuseriState whether the following statements are true or false Give reasons to justify your answers (a) The degree of polynomial 5 x5 6 x4 8 x2 is 4 (b) The algebraic expression is a polynomial (c) The polynomial is a quadratic trinomial Using the long division method, determine the remainder when the polynomial 4 x5 2 x4 x3 4 x2 7




Class 9ncert Solutionschapter 2 Polynomialsexercise 2 5 Solve All Questions And Give Me Answersplease Brainly In




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities In Hindi
Algebraic Expressions and Identities Formulas for Class 8 Maths Chapter 9 Are you looking for Algebraic Expressions and Identities formulas or important points that are required to understand Algebraic Expressions and Identities for class 8 maths Chapter 9?Mathematics NCERT Grade 9, Chapter 2 Polynomials Polynomials are a particular type of algebraic expressionStudents will also study the remainder theorem and factor theorem in this chapterSome more algebraic identities will be discussed in this chapterTheir use in factorisation and in evaluating some given expressions will also be discussed Different polynomials based on the number ofAnswers (1) 12 Step 1 Let's assume the two numbers be x and y Step 2 It is given that, sum of their squares is 25 Therefore, x2 y2 = 25 (1) Step 3 Also the sum of the numbers is 7




Given Three Polynomials X Y Z Which Identity Is True Youtube




Polynomials Important Questions Of Identities Algebraic Identities Class 9 Oda Class Youtube
Solution 5 (i) 2 x 2 x is a quadratic polynomial as its degree is 2 (ii) x x 3 is a cubic polynomial as its degree is 3 (iii) y y 2 4 is a quadratic polynomial as its degree is 2 (iv) 1 x is a linear polynomial as its degree is 1 (v) 3t is a linear polynomial as its degree is 1Ex 25 Class 9 Maths Question 12 Verify that x 3 y 3 z 33xyz = (x y z)(x y) 2 (yz) 2 (zx) 2 Solution We have, x 3 y 3 z 3 – 3xyz = (x y z) x 2 y 2 z 2 – xy – yz – zx = (x y z)2x 2 2y 2 2z 22xy2yz 2zx = (x y z)x 2 x 2 y 2 y 2 z 2 z 22xy2yz2zx = (x y z)x 2 y 2 – 2xy yPolynomials Exercise 25 Part 1 Question 1 Use suitable identities to find the following products (i) `(x 4)(x 10)` Answer Given, `(x 4)(x 10)` We know that, `(x a)(x b) = x^2 (a b) x
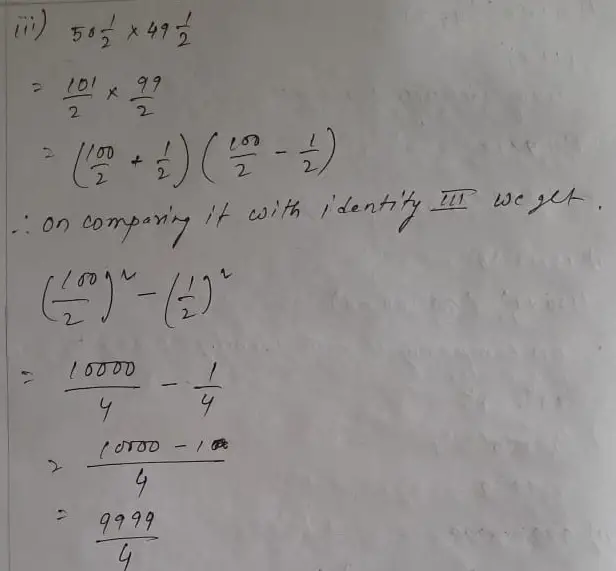



Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5




X3 Y3 Class 9 Maths Algebra Identity Derivation Youtube
The algebraic identities for class 9 consist of identities of all the algebraic formulas and expressions You must have learned algebra formulas for class 9, which are mathematical rule expressed in symbols but the algebraic identities represent that the equation is true for all the values of the variables For example;The perfect cube forms ( x y) 3 (xy)^3 (xy)3 and ( x − y) 3 ( xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 ( x − y) 3 = x 3 − 3 x 2 y 3 Q4 Expand each of the following, using suitable identities (i) (x 2y 4z) 2 (ii) (2x – y z) 2 (iii) (–2x 3y 2z) 2 (iv) (3a – 7b – c) 2 (v) (–2x




X Cube Y Cube Identity X Cube Y Cube Identity Exercise 2 5 Class 9 Q9 Youtube



Geometrical Explanation Of A B C 2 Algebraic Identity Proof Derivation Math Project Youtube
We shall use the identity xy x y = x 2y 2 Here By applying in identity we get Hence the value of is (iv) The given expression is We have So we can express and in the terms of 100 as We shall use the identity xy x y = x 2y 2 Here By applying in identity




5 Extra Questions For Class 9 Maths Chapter 2 With Solution Polynomials Zeroes Remainder Theorem Factorization And Algebraic Identities




Expanding Algebraic Expressions Using Identities Worksheets




Composite Functions And Invertible Function Concepts Videos Examples




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5




Algebraic Expressions Definition Types Formulas




Http Www Aplustopper Com Solving A Quadratic Equation By Factoring Quadratics Maths Solutions Quadratic Equation




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5




Degree Of Polynomials Class 9 Ex 2 1 Q4 Ncert Solution Polynomials Basic Concepts Youtube




How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com




Factorise The Following Using Appropriate Identities I 9x2 6xy Y2 Youtube




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Cbsetuts Com



Class 8 Algebraic Expressions And Identities Jsunil Tutorial Cbse Maths Science




Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks
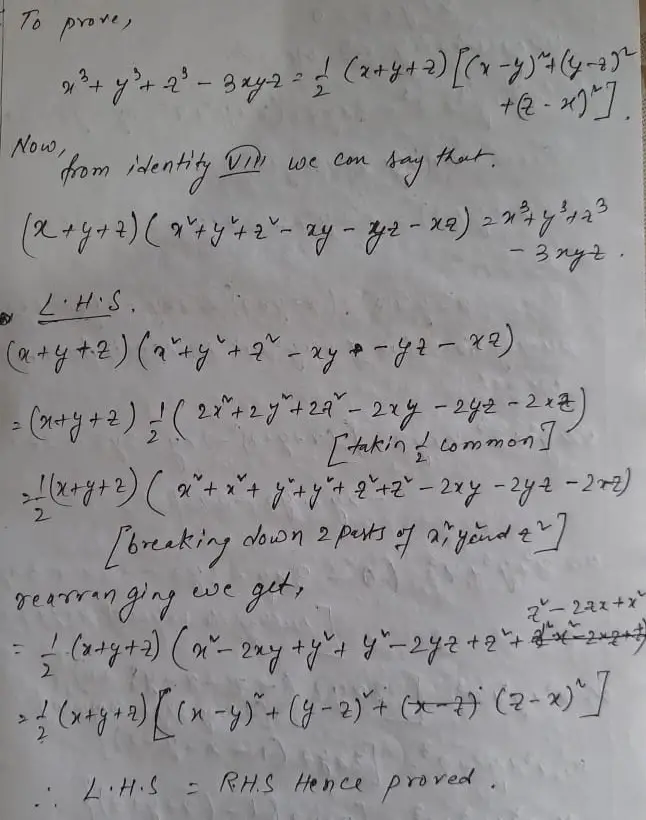



Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5
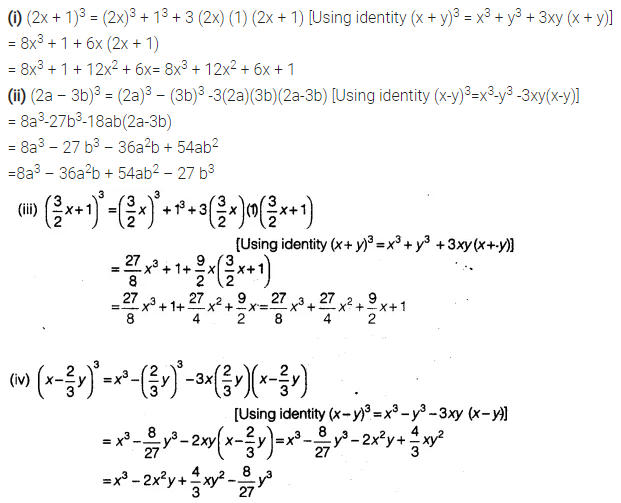



Write The Following Cubes In Expanded Form Cbse Class 9 Maths Learn Cbse Forum




Example 11 Using The Identity I Find I 2x 3y 2 Ii 103 2



Expand 1 X Y 3 Whole Cube Studyrankersonline




1ogcupyd3xwk2m




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com
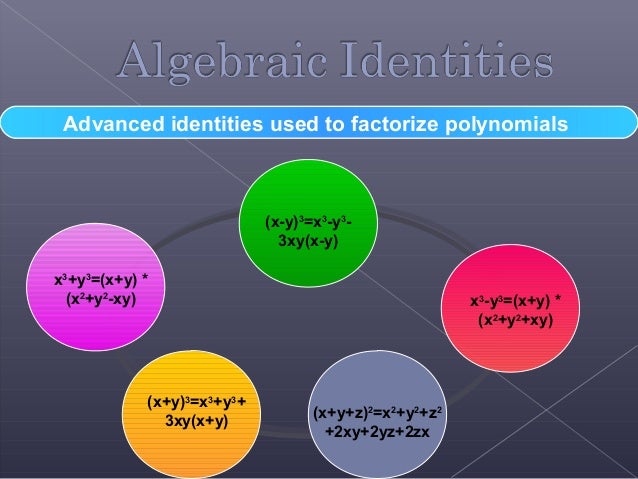



Maths Polynomials 9th




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials




Ex 2 5 9 Verify I X3 Y3 X Y X2 Xy Y2 Ex 2 5




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf




Use Suitable Identities To Find The Following Products I X 4 X 10 Ii X 8 X 10 Ii Youtube




Chapter 4 Algebraic Identities Rd Sharma Solutions For Class 9 Mathematics Cbse Topperlearning




Algebraic Identities Of Polynomials A Plus Topper




Algebraic Identities Of Polynomials A Plus Topper
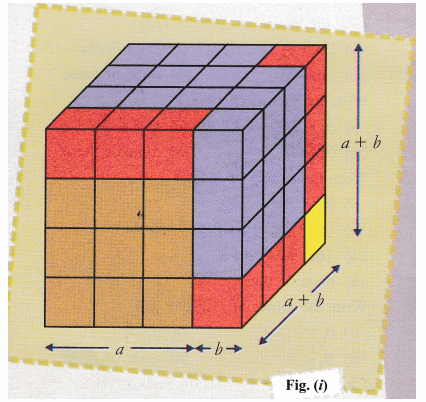



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf




Ncert Solutions For Class 8 Maths Algebraic Expressions And Identities Ex 9 4 Algebraic Expressions Class 8 Expressions
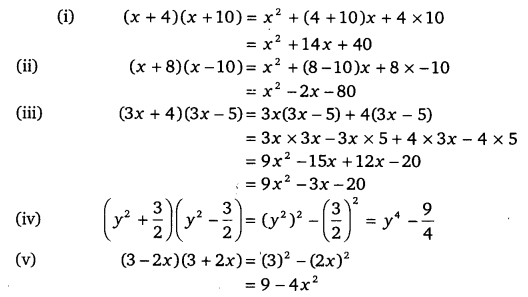



Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com



1



What Is The Answer Of X Y Quora




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5




Use A Suitable Identity To Get Each Of The Following Products I



Q Tbn And9gcrgivwzgq1vicrsz H9kteoigv327j0 I5yvphzqeyx27vc9ra Usqp Cau
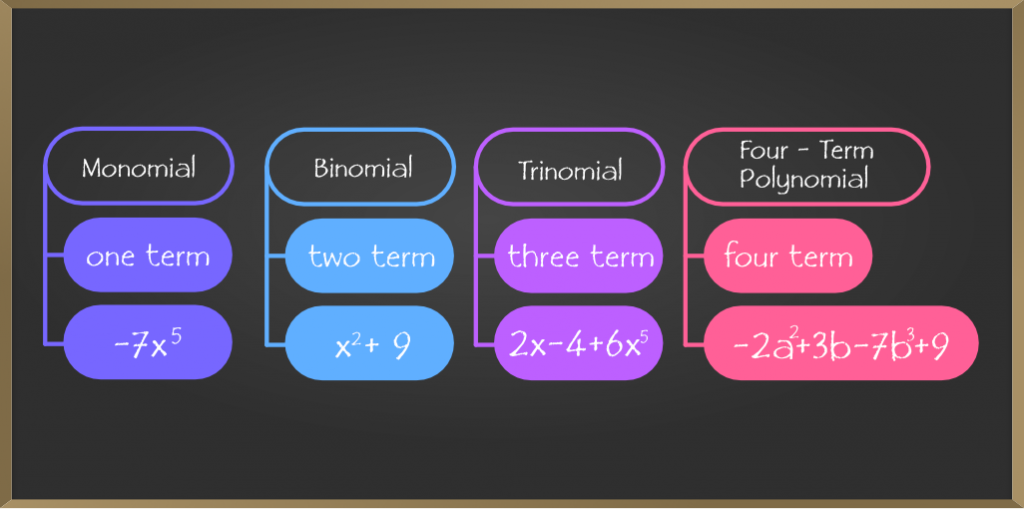



Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks




Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy




Factorisation Using Identities Factoring Algebraic Expressions Examples




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5




Selina Concise Mathematics Class 8 Icse Solutions Chapter 12 Algebraic Identities Cbse Tuts
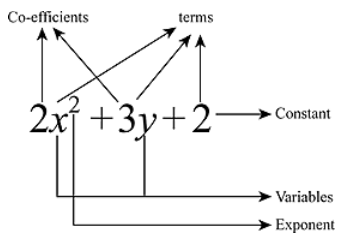



Revision Notes For Maths Chapter 2 Polynomials Class 9th Askiitians




Identity Property Of 0 Video Khan Academy




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5




Factorisation Using Identities Factoring Algebraic Expressions Examples
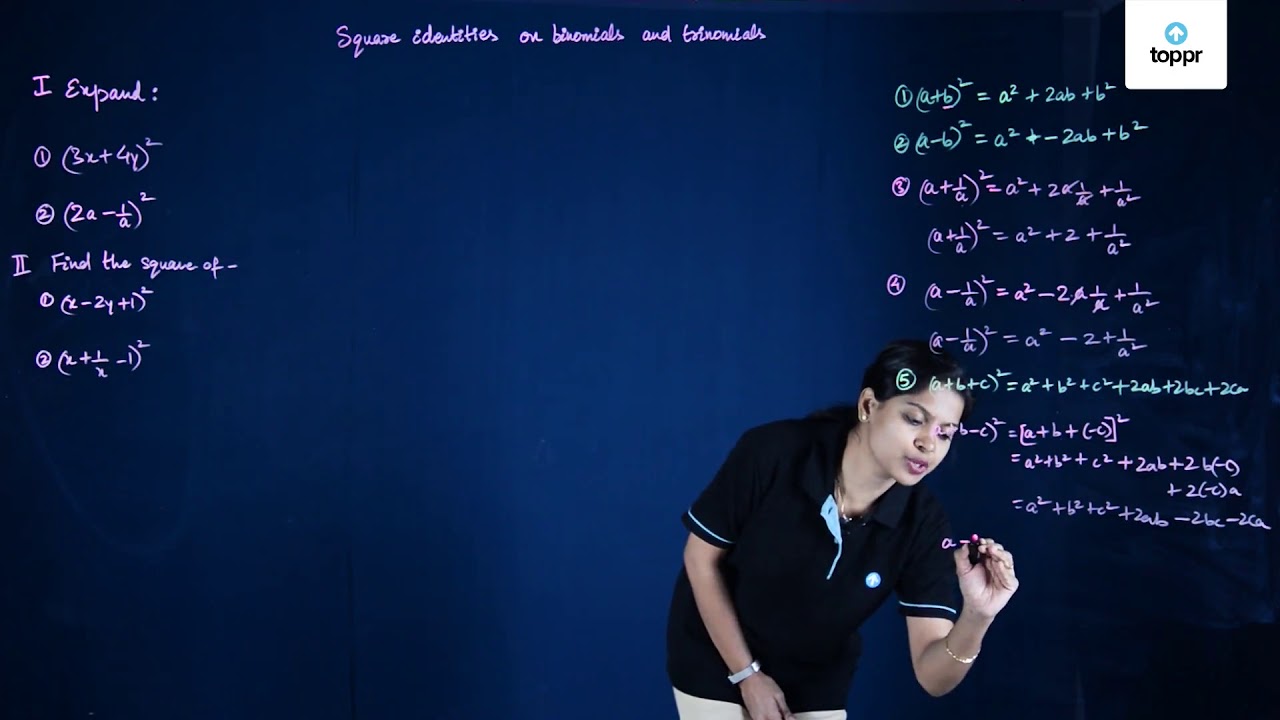



Standard Identities Of Binomials And Trinomials Equations Examples
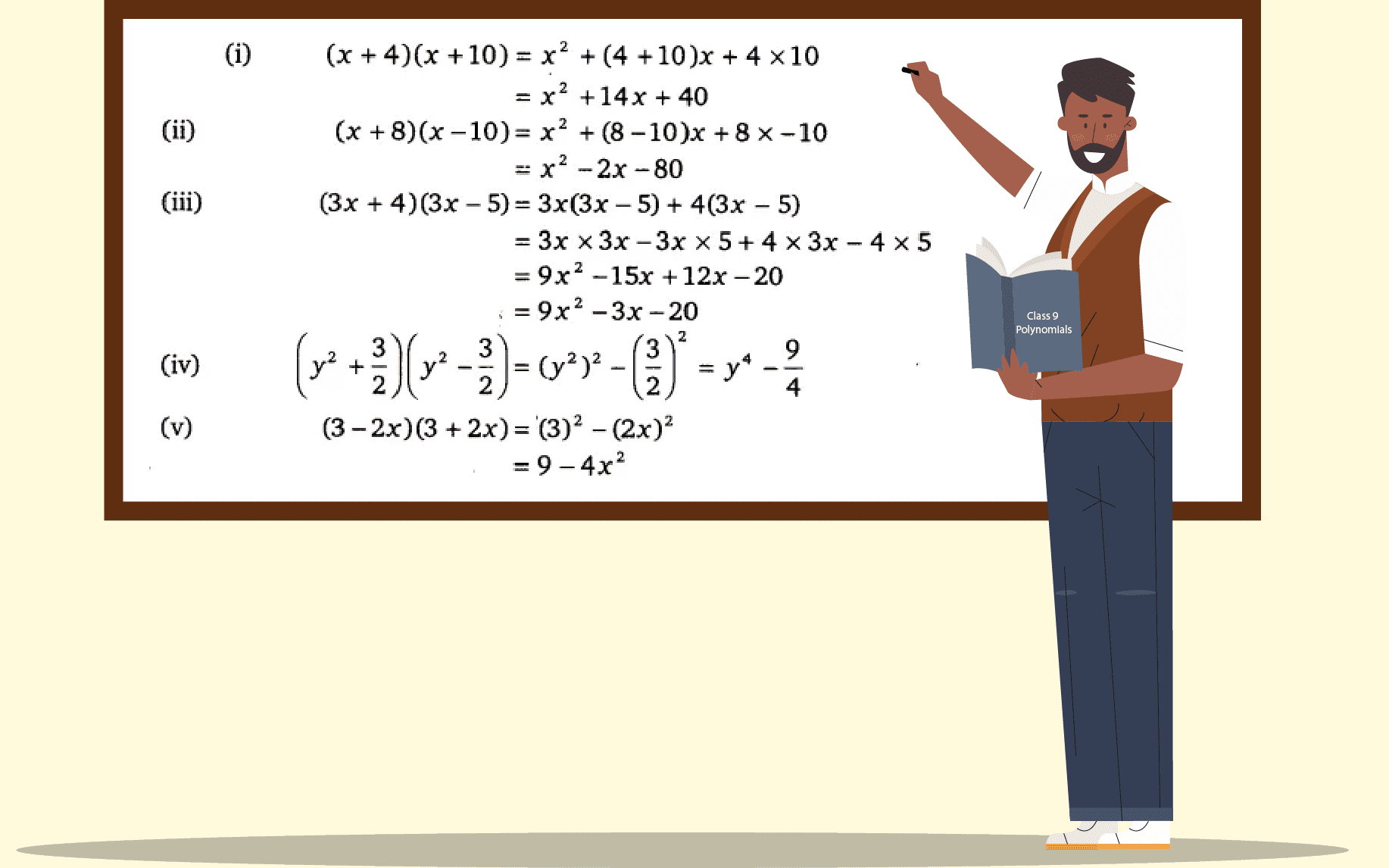



Class 9 Polynomials Study Notes And Important Questions Leverage Edu



1




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5



Q Tbn And9gctu6yibvbesgxnsam965gftocxk9qqmiuojj1wyvdws7eyabnsf Usqp Cau




Algebra Formulas List Of Important Algebraic Expressions Formulas




Expanding Algebraic Expressions Using Identities Worksheets




Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities




Algebraic Identities Of Polynomials A Plus Topper




Algebraic Identities Of Polynomials A Plus Topper



2




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




X 3 Y 3 X 3 Y 3 Formula Proof Youtube




Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities




All Identities Of Class 9 Maths Ch 2 Polynomial Brainly In




Maths Polynomials 9th




Fgszz5fxjmnqm




Cbse Class 9 Algebraic Identities Offered By Unacademy
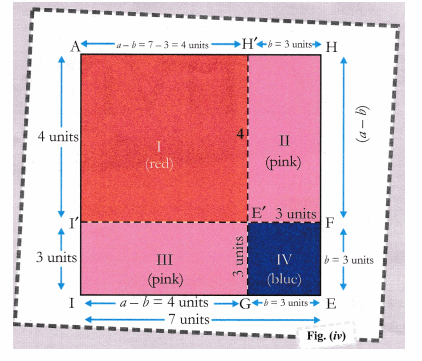



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 2 2ab B2




Standard Identities Of Binomials And Trinomials Equations Examples




Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8




Dcmc Math Class 8 List Of Algebraic Identities For Class 9




Algebraic Identities Standard Algebraic Identities Definition Examples




Gyanpub Learning Polynomials Class 9 Extra Questions Maths Chapter
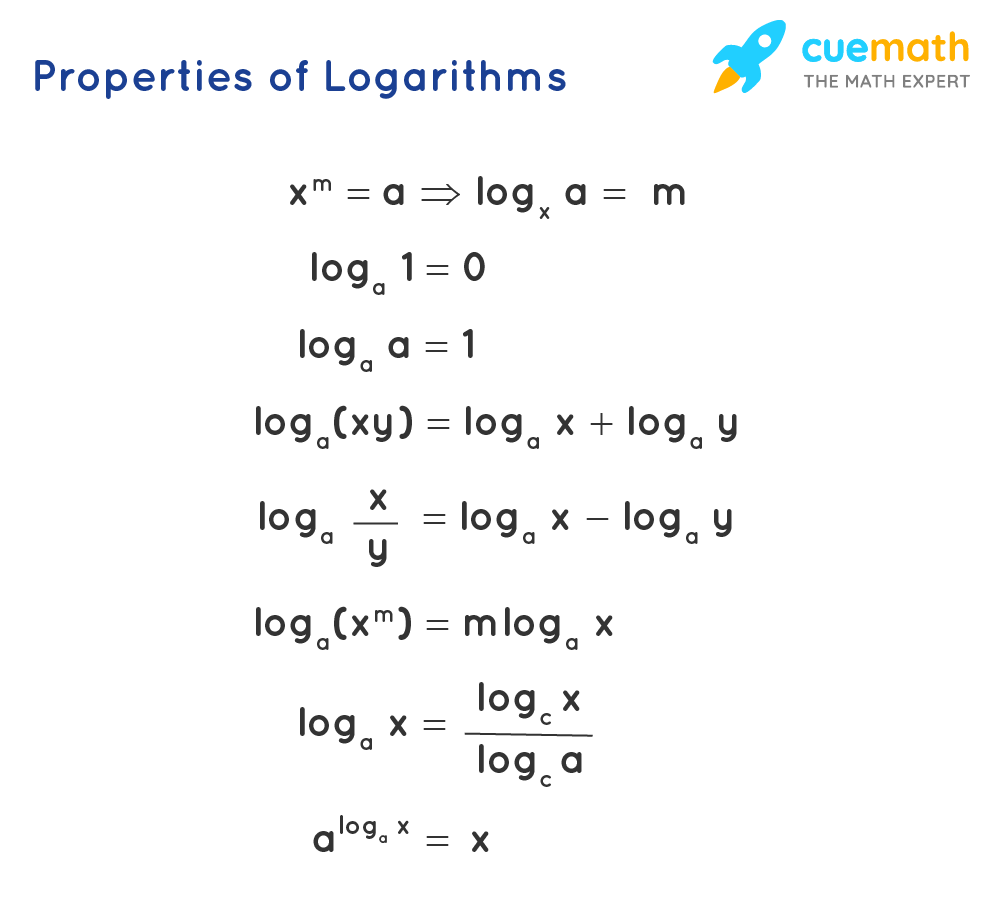



Algebra Formula Solved Examples List Of Algebraic Formulas




Standard Identities Of Binomials And Trinomials Equations Examples




Rd Sharma Class 9 Solutions Algebraic Identities Exercise 4 3 8 Rdsharmaclass9 Class9solutions Rdsharmaclass9solutions Rd Math Notes Solutions Class




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube




Algebraic Expressions Polynomials Cbse Class 9 Ix Mathematics Youtube




Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com




Rd Sharma Class 9 Chapter 4 Algebraic Identities Free Pdf




Class 9ncert Solutionschapter 2 Polynomialsexercise 2 5 Solve All Questions And Give Me Answersplease Brainly In




Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 5 Kseeb Solutions



0 件のコメント:
コメントを投稿